Summary
Lie algebra is useful in the SLAM problem. If the results of the map and pose are to be more accurate, an optimization problem is usually involved, and this optimization problem is often related to the solid body rotation or transformation matrix. But $SO(3)$ and $SE(3)$ do not satisfy the addition operation, that is, when $SO(3)$ or $SE(3)$ is used as optimization variable, it cannot be differentiated. Here Lie algebra plays the role.
Derivatives on Lie groups
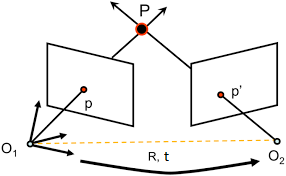 As picture shows point $P$ is observed at camera frame $O_1$ and $O_2$. Offset from $O_1$ to $O_2$ is $[R,T]$. Let's consider coordination of $P$ in frame $O_2$ is $P'$ and we want to calculate its derivative about transformation $T=[R,t]$. Note this problem is equivalent to apply $T^{-1}$ to P in frame $O_1$.
As picture shows point $P$ is observed at camera frame $O_1$ and $O_2$. Offset from $O_1$ to $O_2$ is $[R,T]$. Let's consider coordination of $P$ in frame $O_2$ is $P'$ and we want to calculate its derivative about transformation $T=[R,t]$. Note this problem is equivalent to apply $T^{-1}$ to P in frame $O_1$.
Let $\xi$ be $T$ 's corresponding Lie Algebra and use perturbation model $\delta{\xi}=[\delta{\rho},\delta{\phi}]$.

With this equation, we can optimize camera pose.
0 Comments